Petitverse

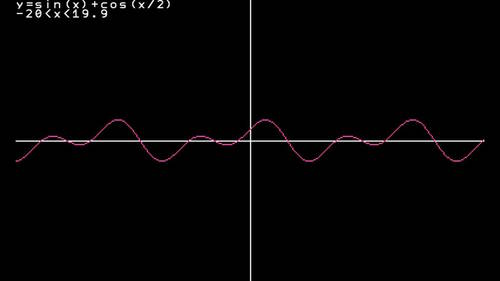
使い方は簡単で表示したい式（Xで表された式）を入力するだけです。一次関数だろうと三角関数だろうと関係なく式を入力するだけでグラフ表示ができます。
そのためには式の評価を行うプログラムが必要不可欠になります。
前回の簡易関数電卓JHでもこれと同等の処理を行っています。
http://petitverse.hosiken.jp/community/petitcom/diary/?read=3579
しかし、この簡易グラフJHではループ内で無数にその処理を行うため自作関数F(X)を作り、それでその処理を行っています。
その自作関数を含めて1画面プログラムJH規格（MAX336文字）の範囲内で作っています。

公開キー【 4X2KX22NE 】

グラフの拡大・縮小やスクロール機能を使うことで、任意の方程式の大雑把な解を知ることができます。

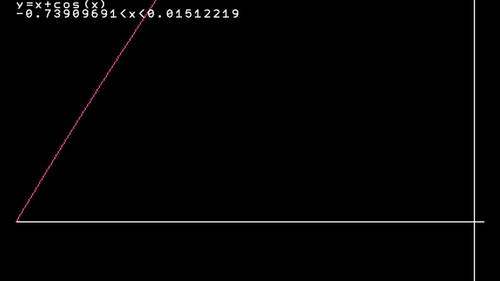
例えば、x+cos x=0 のxの解はy=x+cos(x) と入力してグラフのX軸との交点座標を読み取ることで分かります。
拡大機能を使えば、上記の方程式の解はx≒-0.74であることが分かります。


この短さでは驚異的な性能を持つグラフプログラムですが、いくつかの問題点があります。

(1)描画範囲にプチコン4で求めることができない値が出てきた際にはグラフが表示できない。
(2)不連続なグラフでも連続した線で結ばれる
(3)最初に拡大縮小操作をした際には原点の位置が動く

(1)は例えば円の方程式の上半分部分を表示するy=sqr(100-x*x)という方程式でグラフの初期状態でxの範囲は-20<x<19.9であるためxの絶対値が10を超えてしまいこのグラフは表示できません。
とはいえ、ほとんどのグラフでは問題なく表示できます。

(2)は例えばy=x mod 4というグラフを表示すると階段状のグラフになるのですが、正しく描画する場合にはグラフの縦線の部分は表示しません。
とはいえ、それを分かっていて使うならば問題ないと思います。

(3)は最初に使用する場合は、TOUCH関数では前回タッチした場所が記録されているためです。解決が困難な(1)(2)とは異なり、(3)はタッチしたかどうかを事前に判定すれば簡単に解決できるのですが、このJH規格の範疇では実現が不可能でした。
とはいえ、特に支障はないと思います。