プチコン 非公式コミュニティ
プレイ日記
こういち
◆ou0jbJnEJ0Kb
2020/3/6 22:58 ネタバレ
2020/3/6 22:58 ネタバレ
非負整数Nが与えられたとき、Nがゾロ目かどうかを対数時間で求めたい。
コメント
こういち
2020/3/6 23:02
◆ou0jbJnEJ0Kb
まず、思い付いたのが、
N-N DIV 100000と(N DIV100000)*100000
を比較すれば、数の左右が等しいかどうか分かる。
それを再帰的に適用すれば、ゾロ目かどうか判定できると考えた。
N-N DIV 100000と(N DIV100000)*100000
を比較すれば、数の左右が等しいかどうか分かる。
それを再帰的に適用すれば、ゾロ目かどうか判定できると考えた。
こういち
2020/3/6 23:05
◆ou0jbJnEJ0Kb
これ。桁数が予め分かっていれば、使えるけど、未知の桁数だと上手くいかない。
桁数を求めれば行けるけど、桁数を求めるのにO(log(k))必要なので、全体でO(log(k)^2)
計算量的には悪くはないけど、プチコン扱える整数は10桁程度なので、まだ線形時間で計算した方が速い。
ちなみに数学関数を定数時間とは認めない派です。
桁数を求めれば行けるけど、桁数を求めるのにO(log(k))必要なので、全体でO(log(k)^2)
計算量的には悪くはないけど、プチコン扱える整数は10桁程度なので、まだ線形時間で計算した方が速い。
ちなみに数学関数を定数時間とは認めない派です。
Na
2020/3/6 23:44
◆QoELVrBXBQCI
ゾロ目って、すべての桁が同じ数字ってことですよね?
10で割り続けながら1の位を調べる、というのを考えたんですが
LASTNUM=N MOD 10
N=N DIV 10
ZORO=1
WHILE N>0
IF LASTNUM!=N MOD 10 THEN ZORO=0:BREAK
N=N DIV 10
WEND
10で割り続けながら1の位を調べる、というのを考えたんですが
LASTNUM=N MOD 10
N=N DIV 10
ZORO=1
WHILE N>0
IF LASTNUM!=N MOD 10 THEN ZORO=0:BREAK
N=N DIV 10
WEND
ツララ
2020/3/7 0:41
◆ArUdBYOYME1V
一旦文字列に変換して端の数字と一個ずつ順番に比較してやればいいんじゃないんです？
対象は0以上の整数ですよね。
ゾロ目かどうかを確認したい数をN%とすると
DEF ZOROME(N%)
IF N%<0 THEN RETURN 0 '←負数を除外
VAR M$=STR$(N%),P=LEN(M$),A$=LEFT$(M$,1),I
IF P<2 THEN RETURN 0 '←１桁の数字なら除外
FOR I=1 TO P-1
IF A$!=MID$(M$,I,1) THEN BREAK
NEXT
RETURN I>P-1
END
みたいな処理で判定できません？
対象は0以上の整数ですよね。
ゾロ目かどうかを確認したい数をN%とすると
DEF ZOROME(N%)
IF N%<0 THEN RETURN 0 '←負数を除外
VAR M$=STR$(N%),P=LEN(M$),A$=LEFT$(M$,1),I
IF P<2 THEN RETURN 0 '←１桁の数字なら除外
FOR I=1 TO P-1
IF A$!=MID$(M$,I,1) THEN BREAK
NEXT
RETURN I>P-1
END
みたいな処理で判定できません？
こういち
2020/3/7 1:10
◆ou0jbJnEJ0Kb
Naさん
ツララさん
速度を気にしないのならそれで判定できますね。
というか10桁程度なので下手に計算量改善するより線形時間で判定した方が速い可能性すらあります。
それでも少しでも速くしたいと思って投稿しました。
ツララさん
速度を気にしないのならそれで判定できますね。
というか10桁程度なので下手に計算量改善するより線形時間で判定した方が速い可能性すらあります。
それでも少しでも速くしたいと思って投稿しました。
SatoshiMcCloud
2020/3/7 8:30
◆Z1qfV11i63Jr
ジャッジする変数が整数型と仮定します。
変数が取りうる値は、非負という条件から0から21,4748,3647となります。
この中でゾロ目になるパターンは、
・2桁のとき・・・9パターン
・3桁のとき・・・9パターン
…
・10桁のとき・・・1パターン
全部で73パターンしかありません。
だから、
if(N==11)then return true
if(N==22)then return true
…
と、全パターンに対して判定するプログラムを書けばいいと思います。最悪でもif判定73回で済みます。
変数が取りうる値は、非負という条件から0から21,4748,3647となります。
この中でゾロ目になるパターンは、
・2桁のとき・・・9パターン
・3桁のとき・・・9パターン
…
・10桁のとき・・・1パターン
全部で73パターンしかありません。
だから、
if(N==11)then return true
if(N==22)then return true
…
と、全パターンに対して判定するプログラムを書けばいいと思います。最悪でもif判定73回で済みます。
SatoshiMcCloud
2020/3/7 8:35
◆Z1qfV11i63Jr
さらにスピードを求めるなら、二分探索で範囲を絞って判定すればいいと思います。
73<2の7乗なので、if文10回未満で計算できるはず。
73<2の7乗なので、if文10回未満で計算できるはず。
さすらいの名無し
2020/3/7 10:09
◆LWMA5UzCJb3e
KETA=LEN(FORMAT$("%D",N))
IF N MOD VAL("1"*KETA)==0 THEN RSLT=1 ELSE RSLT=0
対数時間とか使ってないけど(対数時間とは？)
IF N MOD VAL("1"*KETA)==0 THEN RSLT=1 ELSE RSLT=0
対数時間とか使ってないけど(対数時間とは？)
ツララ
2020/3/7 13:39
◆ArUdBYOYME1V
ああ、そうか
ゾロ目ってことは桁数が揃っていれば１が連続した数の倍数だから
DEF ZOROME(N)
VAR P
IF N<=0||INSTR(STR$(N),”.”)>=0 THEN RETURN 0
P=LOG(N,10)
IF P<1 THEN RETURN 0 ELSE P=(P OR 0)+1
RETURN INSTR(STR$(N/VAL(“1”*P)),”.”)<0
END
みたいな処理でもいいのか。
ループ処理要らないですね。
MODとかの演算子を使うと強制的に整数型になっちゃうから
整数型の最大値より大きい数にも適用させようとすると、ちょっと工夫が必要ですねコレ。
ゾロ目ってことは桁数が揃っていれば１が連続した数の倍数だから
DEF ZOROME(N)
VAR P
IF N<=0||INSTR(STR$(N),”.”)>=0 THEN RETURN 0
P=LOG(N,10)
IF P<1 THEN RETURN 0 ELSE P=(P OR 0)+1
RETURN INSTR(STR$(N/VAL(“1”*P)),”.”)<0
END
みたいな処理でもいいのか。
ループ処理要らないですね。
MODとかの演算子を使うと強制的に整数型になっちゃうから
整数型の最大値より大きい数にも適用させようとすると、ちょっと工夫が必要ですねコレ。
こういち
2020/3/7 20:04
◆ou0jbJnEJ0Kb
さすらいの名無しさん
対数時間は、入力長(Nの桁数)の対数(桁数)に比例した時間で処理が完了することですね。桁数が倍になっても、処理の回数が数回増える程度の時間。
で、LEN(),VAL(),STR$()は恐らく内部で線形時間(桁数に比例した時間)になってるはず。
それはそうとコードがすっきりしてて好き。
SatoshiMcCloudさん
ふむ。賢い。1桁につき9回の計算なので、線形時間。
にぶたんはどう適用するかイメージできないですが、IF文の回数を見る限り対数時間。
これは採用するしかないですね。
対数時間は、入力長(Nの桁数)の対数(桁数)に比例した時間で処理が完了することですね。桁数が倍になっても、処理の回数が数回増える程度の時間。
で、LEN(),VAL(),STR$()は恐らく内部で線形時間(桁数に比例した時間)になってるはず。
それはそうとコードがすっきりしてて好き。
SatoshiMcCloudさん
ふむ。賢い。1桁につき9回の計算なので、線形時間。
にぶたんはどう適用するかイメージできないですが、IF文の回数を見る限り対数時間。
これは採用するしかないですね。
こういち
2020/3/7 21:48
◆ou0jbJnEJ0Kb
(真面目にやるなら配列でゾロ目一覧持てば良いのでは)
ツララ
2020/3/8 6:15
◆ArUdBYOYME1V
LEN()って引数の文字数に実行速度って影響されないですよ？
あと数値を文字列化するならFORMAT$()の方がSTR$()よりも高速だから
Nが10以上の整数って条件の値しか取らないなら、さすらいさんのが最速になるんじゃないんです？
RSLT=!(N MOD VAL("1"*LEN(FORMAT$("%D",N))))
って一行の式にできちゃいますし。
プチコンのシステム側で設定されてる関数が
引数の数値や文字列の長さで実行速度がどれくらい影響受けるか色々調べてみたら面白いかも。
単なる予測を根拠に便利な関数使わないってのは本末転倒かと。
あと数値を文字列化するならFORMAT$()の方がSTR$()よりも高速だから
Nが10以上の整数って条件の値しか取らないなら、さすらいさんのが最速になるんじゃないんです？
RSLT=!(N MOD VAL("1"*LEN(FORMAT$("%D",N))))
って一行の式にできちゃいますし。
プチコンのシステム側で設定されてる関数が
引数の数値や文字列の長さで実行速度がどれくらい影響受けるか色々調べてみたら面白いかも。
単なる予測を根拠に便利な関数使わないってのは本末転倒かと。
こういち
2020/3/8 14:10
◆ou0jbJnEJ0Kb
確かにLEN()は定数時間ですね。でもFORMAT$()とVAL()がネックになってるのは間違いないので、SatoshiMcCloudさんのコードを採用することになると思います。
速度が欲しいと言うより対数時間のコードが欲しいので。
速度が欲しいと言うより対数時間のコードが欲しいので。
Na
2020/3/8 22:18
◆QoELVrBXBQCI
IF N<100 THEN RETURN !(N MOD 11) '11で割り切れたら1
IF N<1000 THEN RETURN !(N MOD 111)
IF N<10000 THEN RETURN !(N MOD 1111)
...
というのは?
IF判定最大8回+MODの計算1回で済みそうですがどうでしょうか
IF N<1000 THEN RETURN !(N MOD 111)
IF N<10000 THEN RETURN !(N MOD 1111)
...
というのは?
IF判定最大8回+MODの計算1回で済みそうですがどうでしょうか
こういち
2020/3/9 8:07
◆ou0jbJnEJ0Kb
Naさん
IF文が桁数の分必要になるので線形時間ですね。
ただ、にぶたんを使えば対数時間に出来るので使えますね。
IF文が桁数の分必要になるので線形時間ですね。
ただ、にぶたんを使えば対数時間に出来るので使えますね。
Na
2020/3/9 10:17
◆QoELVrBXBQCI
(←対数時間っていうのがNの桁数の対数を指してるということにやっと気づいた人)
じゃあ桁数を二分探索で求めたらどうでしょう。
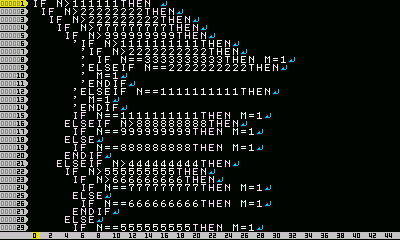
IF N<=1E5 THEN
IF N<=1E3 THEN
IF N<=1E2 THEN RETURN !(N MOD 11) ELSE RETURN !(N MOD 111)
ELSE
IF N<=1E4 THEN RETURN !(N MOD 1111) ELSE RETURN !(N MOD 11111)
ENDIF
ELSE
IF N<=1E7 THEN
IF N<=1E6 THEN RETURN !(N MOD 111111) ELSE RETURN !(N MOD 1111111)
ELSE
IF N<=1E8 THEN
RETURN !(N MOD 11111111)
ELSE
IF N<=1E9 THEN RETURN !(N MOD 111111111) RETURN !(N MOD 1111111111)
ENDIF
ENDIF
最大IF4回+MOD1回です
じゃあ桁数を二分探索で求めたらどうでしょう。
IF N<=1E5 THEN
IF N<=1E3 THEN
IF N<=1E2 THEN RETURN !(N MOD 11) ELSE RETURN !(N MOD 111)
ELSE
IF N<=1E4 THEN RETURN !(N MOD 1111) ELSE RETURN !(N MOD 11111)
ENDIF
ELSE
IF N<=1E7 THEN
IF N<=1E6 THEN RETURN !(N MOD 111111) ELSE RETURN !(N MOD 1111111)
ELSE
IF N<=1E8 THEN
RETURN !(N MOD 11111111)
ELSE
IF N<=1E9 THEN RETURN !(N MOD 111111111) RETURN !(N MOD 1111111111)
ENDIF
ENDIF
最大IF4回+MOD1回です
こういち
2020/3/9 14:11
◆ou0jbJnEJ0Kb
Naさん
それなら対数時間ですね。
しかも、コードも長くならず、昔書いた｢最上位以外の桁が0かどうか｣のコードを再利用できるので、理想的です。
ありがとうございます。
それなら対数時間ですね。
しかも、コードも長くならず、昔書いた｢最上位以外の桁が0かどうか｣のコードを再利用できるので、理想的です。
ありがとうございます。
ツララ
2020/3/9 19:23 ネタバレ
◆ArUdBYOYME1V
高原のな
2020/3/10 10:34 ネタバレ
◆bY8RViwvoODw
Na
2020/3/12 14:35 ネタバレ
◆QoELVrBXBQCI
コメントを書く
- こちらは「プチコン3号」「プチコンBIG」など、プチコンシリーズに関する話題を扱ったコミュニティです
- プチコンシリーズにまったく関係ない書き込みはご遠慮下さい。削除の対象となります
- こちらにはその他のゲームや雑談のコミュニティはなく、作る予定もありません (ひとりで管理できないため)。ごめんなさい
- ユーザー登録なしで書き込みができます
- 秘密の合い言葉は成りすましの防止 (トリップ機能)、書き込みの編集時の本人認証に使用します
- 秘密の合い言葉に他人に推測されやすい言葉、他サービスと同じパスワードは入力しないでください。
- 書き込むと、投稿時に入力したお名前と秘密の暗号が記憶され、ログイン状態になります