Petitverse

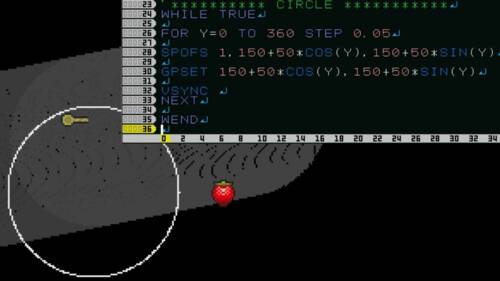
高校数学の数IIIの媒介変数表示というものに似た考え方があります。
そのプログラムのSPOFSに少し応用を加えると面白い図形が沢山描けますよ！

(以下、プログラム例)
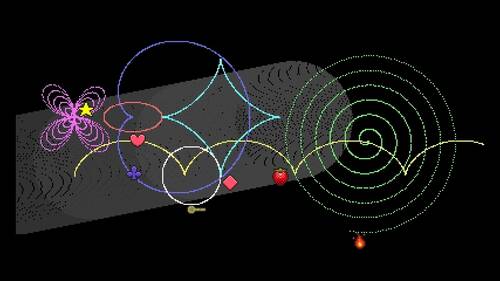
【楕円】
SPOFS 1,150+50*cos(Y),150+50*sin(Y)/2
円を潰したような形です。

【サイクロイド】
SPOFS 1,50+15*(Y-sin(Y)),150-15*(1-cos(Y))
転がる円の上にある点の軌跡です。
最も早く転がる坂の形状としても有名です。(最速降下曲線で調べてみて下さい)

【アステロイド】
SPOFS 1,150+50*POW(cos(Y),3),100+50*POW(sin(Y),3)
※POW(cos(Y),3) はcos(Y)の3乗という意味です。
星のような形をした曲線です。

【カージオイド】
SPOFS 1,150+50*(1+cos(Y))*cos(Y),100+50*(1+cos(Y))*sin(Y)
ハート型を描く曲線です。面白い形をしています。

「数III いろいろな曲線」で調べるともっとたくさん出てきます。
気になったら是非！

そうです！だいたいそんな感じです
やはり数学は奥が深くて良いですよね…

円形に動かす方法。色々ありますね。
その中でも三角関数は直感的で並列化にも強いのが魅力

他にはフックの法則、複素数の累乗など
ブレゼンハムのアルゴリズムなんてのもあったっけ…

円を構成する成分って中心点の座標とその点からの距離だから
件の方程式も三平方の定理から(x-a)^2+(y-b)^2=r^2って形から変形すれば
x^2+y^2+2a*x+2b*y+(a^2+b^2-r^2)=0だけど
ここからX=とY=の式を導き出すなら展開しない方が楽ですな
（　X=a±√r^2-(y-b)^2　と　Y=b±√r^2-(x-a)^2　）
んでFOR文使って４つの象限毎に走査する軸をXとYを切り替えて
FOR X=0 TO R STEP 1
Y=b+√r^2-(x-a)^2
SPOFS
NEXT
FOR Y=0 TO -R STEP -1
X=a-√r^2-(y-b)^2
・
・
みたくやれば
直線を描く要領で座標を求めれて別に三角関数使わなくてもよかったり

・・・そもそも”=”を使わないと方程式じゃないんじゃないんです？

沼った原因はどうでもよくて結果だけ欲しいなら関連書籍漁った方が近道ですよ