プチコン 非公式コミュニティ
トピック
プチコン 非公式コミュニティ
トピック
bはかせ
◆fgfPl6qLuzIU
2017/12/27 17:27
2017/12/27 17:27
質問
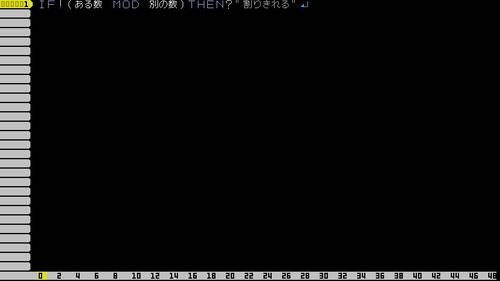
割りきれるかどうか判断したい
ある数を別の数で割るときに
少数がでないかどうか判断したいのですが
いい方法はないでしょうか
少数がでないかどうか判断したいのですが
いい方法はないでしょうか
コメント
こういち
2017/12/27 18:48
◆ou0jbJnEJ0Kb
その別の数が
1<<nで表せる数(2,4,8,16,32,64…)
の場合
if(ある数 and 別の数-1)==0 then 〜
でも行けたりします。
1<<nで表せる数(2,4,8,16,32,64…)
の場合
if(ある数 and 別の数-1)==0 then 〜
でも行けたりします。
しんいち
2017/12/27 19:59
◆lHy.hAWXbthn
整数ならMODで簡単にできるけど、実数でもとなると工夫が必要か。
因みに
1.5 MOD 0.25
はDivide by zeroでエラーになっちゃいますね。
因みに
1.5 MOD 0.25
はDivide by zeroでエラーになっちゃいますね。
bはかせ
2017/12/27 21:12
◆fgfPl6qLuzIU
へー MOD...
MODって使ったことなかったんですが
余りを取得する命令だったんですね。
いろんな用法を教えてくださりありがとうございます。
質問続けになってしまうのですが、
0になるまで割りきれなくてもいいので、
ある数が別の数を割れるかどうか(少数がでないか)を
確かめるのにはどうしたらいいでしょうか?
MODって使ったことなかったんですが
余りを取得する命令だったんですね。
いろんな用法を教えてくださりありがとうございます。
質問続けになってしまうのですが、
0になるまで割りきれなくてもいいので、
ある数が別の数を割れるかどうか(少数がでないか)を
確かめるのにはどうしたらいいでしょうか?
キルル2
2017/12/27 21:50
◆rGE712Ruejv7
割ったときに少数が出るかどうかを判断するなら
実際に割ってみて
少数が出たら少数が出る
出なかったら少数は出ない
とか?
少数が出たかどうかは(n-(n<<0))で判断できます
演算誤差とやらが現れそうですが
実際に割ってみて
少数が出たら少数が出る
出なかったら少数は出ない
とか?
少数が出たかどうかは(n-(n<<0))で判断できます
演算誤差とやらが現れそうですが
こういち
2017/12/27 21:51
◆ou0jbJnEJ0Kb
ボクの睡魔が限界まで来てるせいか質問の内容が頭に入ってこない…。
def gcd(n,m)
if(n mod m==0) return m
return gcd(m,n mod m)
end
↑は質問の回答とは一切関係ありません。多分。
def gcd(n,m)
if(n mod m==0) return m
return gcd(m,n mod m)
end
↑は質問の回答とは一切関係ありません。多分。
bはかせ
2017/12/27 22:14
◆fgfPl6qLuzIU
あれ すみません自分で自分の言ってることが
よくわかりません
ちょっと眠いので顔洗ってきます
よくわかりません
ちょっと眠いので顔洗ってきます
bはかせ
2017/12/27 22:26
◆fgfPl6qLuzIU
顔は洗ってませんが目は覚めてきました
自分の求めている答えは最初の答えで十分でした
ある数を別の数で割ったときにその余りが出るか
出ないか調べたい、と言おうと思ってたのだとおもいます
訳のわからない質問にも回答していただき
ありがとうございます。
自分の求めている答えは最初の答えで十分でした
ある数を別の数で割ったときにその余りが出るか
出ないか調べたい、と言おうと思ってたのだとおもいます
訳のわからない質問にも回答していただき
ありがとうございます。
こういち
2017/12/27 22:40
◆ou0jbJnEJ0Kb
なるほど。そういう意味でしたか。すっきりしました。
後上のプログラム、C言語の癖が抜けてなかったようで間違ってました。
正しくは
def gcd(n,m)
if(n mod m==0)then return m
return gcd(m,n mod m)
end
後上のプログラム、C言語の癖が抜けてなかったようで間違ってました。
正しくは
def gcd(n,m)
if(n mod m==0)then return m
return gcd(m,n mod m)
end
おちゃめ
2017/12/29 1:09
◆jH1opV6FnGyx
割り切れるかどうかの判定は整数値であればMODで簡単に判定が可能です。
しかし、実数値ではMODでは判定ができません。
というのもMODでは引数を整数型に変換して演算が行われるためです。
したがって、1.5 MOD 0.25 は 1 MOD 0 として計算されるわけです。
ならば。両者を100倍して150 MOD 25 として計算すれば良さそうですが、そういう単純にはなかなかいかないのです。(小数値を10倍してもぴったり10倍にはなるわけではない)
それはプチコン3号に限らず多くのコンピュータは内部では2進数で計算されているためです。
0.1という見た目でキリの良い値であっても2進数では循環小数となっているためプチコン3号で0.1を正しい値で扱うことができません。(あくまで「0.1に限りなく近い値」であり、実際は丸め処理によってわずかに0.1とは異なる値となっている)
このわずかな誤差によって例えば0.1を9回足した値は0.9とは明確に異なる値となります。(A=0:FOR I=1 TO 9:A=A+0.1:NEXTとしてAと0.9を比較演算してみるとわかる)
したがって、「割り切れるかどうか」を整数型だけではなく実数型に拡張するならば「(整数値に変換して)実際に割ってみてぴったり割り切れるかどうか」よりも「わずかな誤差を許容する仕組み」を採り入れるのがベターだと私は思います。
実数型で発生するわずかな誤差の問題については私のサイトの講座を参考にしてみてください。
http://ochameclub.web.fc2.com/petitcom3/lecture/floating_point_error.htm
しかし、実数値ではMODでは判定ができません。
というのもMODでは引数を整数型に変換して演算が行われるためです。
したがって、1.5 MOD 0.25 は 1 MOD 0 として計算されるわけです。
ならば。両者を100倍して150 MOD 25 として計算すれば良さそうですが、そういう単純にはなかなかいかないのです。(小数値を10倍してもぴったり10倍にはなるわけではない)
それはプチコン3号に限らず多くのコンピュータは内部では2進数で計算されているためです。
0.1という見た目でキリの良い値であっても2進数では循環小数となっているためプチコン3号で0.1を正しい値で扱うことができません。(あくまで「0.1に限りなく近い値」であり、実際は丸め処理によってわずかに0.1とは異なる値となっている)
このわずかな誤差によって例えば0.1を9回足した値は0.9とは明確に異なる値となります。(A=0:FOR I=1 TO 9:A=A+0.1:NEXTとしてAと0.9を比較演算してみるとわかる)
したがって、「割り切れるかどうか」を整数型だけではなく実数型に拡張するならば「(整数値に変換して)実際に割ってみてぴったり割り切れるかどうか」よりも「わずかな誤差を許容する仕組み」を採り入れるのがベターだと私は思います。
実数型で発生するわずかな誤差の問題については私のサイトの講座を参考にしてみてください。
http://ochameclub.web.fc2.com/petitcom3/lecture/floating_point_error.htm
コメントを書く
- こちらは「プチコン3号」「プチコンBIG」など、プチコンシリーズに関する話題を扱ったコミュニティです
- プチコンシリーズにまったく関係ない書き込みはご遠慮下さい。削除の対象となります
- こちらにはその他のゲームや雑談のコミュニティはなく、作る予定もありません (ひとりで管理できないため)。ごめんなさい
- ユーザー登録なしで書き込みができます
- 秘密の合い言葉は成りすましの防止 (トリップ機能)、書き込みの編集時の本人認証に使用します
- 秘密の合い言葉に他人に推測されやすい言葉、他サービスと同じパスワードは入力しないでください。
- 書き込むと、投稿時に入力したお名前と秘密の暗号が記憶され、ログイン状態になります