プチコン 非公式コミュニティ
トピック
しんいち
◆lHy.hAWXbthn
2021/1/7 18:11
2021/1/7 18:11
質問
玉を跳ね返したい(反射角)
タッチで引いた線で玉を跳ね返したい。けど、跳ね返す角度の計算がよく分からん。と言うことで、お知恵を拝借させて下さいませ。
引いた線を GLINE X1,Y1,X2,Y2,-1 とすると
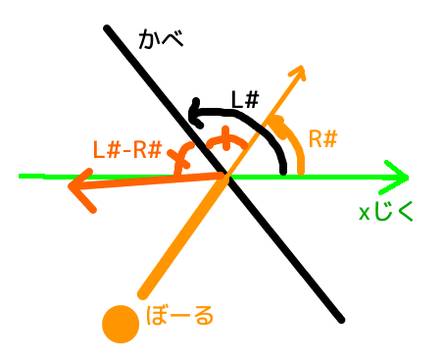
線の角度は L#=ATAN(Y2-Y1,X2-X1) 'X,Yの順番／符号これで良い？
玉のX座標,Y座標の移動量(速度)を X#,Y# とすると
玉の角度は R#=ATAN(Y#,X#)
L# と R# から反射角求まるかな？
反射角が分かれば X#=COS(R#)*V:Y#=SIN(R#)*V 'Vは玉の速度
として、めでたしめでたし。
サンプルも用意しました(文章だけじゃ分からんよね)。
公開キー：XBCE788E (3号/BIG用)
ファイル：REF_TEST0
4でもXSCREEN/DISPLAY/VISIBLE削ってBUTTON関係直せば動くと思う。
44行目が該当箇所。35行目も関係あるかな。
＃久々にBIGいじってあたふた^^;
引いた線を GLINE X1,Y1,X2,Y2,-1 とすると
線の角度は L#=ATAN(Y2-Y1,X2-X1) 'X,Yの順番／符号これで良い？
玉のX座標,Y座標の移動量(速度)を X#,Y# とすると
玉の角度は R#=ATAN(Y#,X#)
L# と R# から反射角求まるかな？
反射角が分かれば X#=COS(R#)*V:Y#=SIN(R#)*V 'Vは玉の速度
として、めでたしめでたし。
サンプルも用意しました(文章だけじゃ分からんよね)。
公開キー：XBCE788E (3号/BIG用)
ファイル：REF_TEST0
4でもXSCREEN/DISPLAY/VISIBLE削ってBUTTON関係直せば動くと思う。
44行目が該当箇所。35行目も関係あるかな。
＃久々にBIGいじってあたふた^^;
コメント
Na
2021/1/7 18:32 ネタバレ
◆QoELVrBXBQCI
しんいち
2021/1/7 21:15 ネタバレ
◆lHy.hAWXbthn
こういち
2021/1/8 9:15
◆.Id/aHiU36hu
壁の法線と速度の内積を二倍して、速度に加算するという方法もある。
しんいち
2021/1/8 22:31
◆lHy.hAWXbthn
＞こういちさん
調べてたらその方法も見かけたんですけど、具体的な記述（ソースコード）がイメージできなかった。説明はとってもシンプルに書かれてたんだけど^^;
ちゃんと理解できればそっちの方が演算負荷低そうなんですけどね。
調べてたらその方法も見かけたんですけど、具体的な記述（ソースコード）がイメージできなかった。説明はとってもシンプルに書かれてたんだけど^^;
ちゃんと理解できればそっちの方が演算負荷低そうなんですけどね。
Na
2021/1/8 23:16 ネタバレ
◆QoELVrBXBQCI
しんいち
2021/1/10 20:35 ネタバレ
◆lHy.hAWXbthn
コメントを書く
- こちらは「プチコン3号」「プチコンBIG」など、プチコンシリーズに関する話題を扱ったコミュニティです
- プチコンシリーズにまったく関係ない書き込みはご遠慮下さい。削除の対象となります
- こちらにはその他のゲームや雑談のコミュニティはなく、作る予定もありません (ひとりで管理できないため)。ごめんなさい
- ユーザー登録なしで書き込みができます
- 秘密の合い言葉は成りすましの防止 (トリップ機能)、書き込みの編集時の本人認証に使用します
- 秘密の合い言葉に他人に推測されやすい言葉、他サービスと同じパスワードは入力しないでください。
- 書き込むと、投稿時に入力したお名前と秘密の暗号が記憶され、ログイン状態になります