プチコン 非公式コミュニティ
トピック
プチコン 非公式コミュニティ
トピック
こういち
◆.Id/aHiU36hu
2021/6/15 12:55
2021/6/15 12:55
情報交換
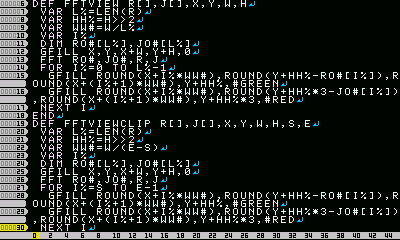
FFT/NTTを極めたい
「書こうと思ったプログラムがFFT/NTT必須だったので諦めた」
みたいなパターンにN回遭遇してるので、そろそろ理解しておきたいです。
理解を深めるため、僕も積極的にコメントしていきますが、「こんなの知ってるよ」みたいな感じのコメント大歓迎です。
とにかくFFT/NTTについて知ってることをコメントしていくトピックです。
みたいなパターンにN回遭遇してるので、そろそろ理解しておきたいです。
理解を深めるため、僕も積極的にコメントしていきますが、「こんなの知ってるよ」みたいな感じのコメント大歓迎です。
とにかくFFT/NTTについて知ってることをコメントしていくトピックです。
コメント
こういち
2021/6/15 12:56
◆.Id/aHiU36hu
フーリエ変換とは
全ての信号(音声などの波形)はいろんな周波数の正弦波の重ね合わせで表現できる
信号を周波数成分に分解する計算をフーリエ変換という。
信号にどの周波数の成分がどれだけ含まれているかの情報に変換する
DFTとは
離散フーリエ変換
現実世界は連続した世界であるため、時間や空間を無限に小さく分割できる
コンピュータの世界ではそうはいかない。画面上に点を打つ時も整数で座標を指定しなければいけない。
無限に続く実数で表せる世界を連続系、整数で表さなければいけない世界を離散系という
離散系でのフーリエ変換を離散フーリエ変換という
全ての信号(音声などの波形)はいろんな周波数の正弦波の重ね合わせで表現できる
信号を周波数成分に分解する計算をフーリエ変換という。
信号にどの周波数の成分がどれだけ含まれているかの情報に変換する
DFTとは
離散フーリエ変換
現実世界は連続した世界であるため、時間や空間を無限に小さく分割できる
コンピュータの世界ではそうはいかない。画面上に点を打つ時も整数で座標を指定しなければいけない。
無限に続く実数で表せる世界を連続系、整数で表さなければいけない世界を離散系という
離散系でのフーリエ変換を離散フーリエ変換という
こういち
2021/6/15 12:57
◆.Id/aHiU36hu
FFTとは
DFTを高速化したやつ
DFTを奇数の信号のみ、偶数の信号のみ取り出してDFTした後、それらを合わせると、元の信号をDFTしたものと同じ結果になる
半分にしたものをさらに半分にして同様なことを繰り返すと、結局普通にDFTするより速くなる
何度もサイズを半分にするので、元のデータがちょうどいい数(1024とか256とか)だとやりやすい
IFFTとは
FFTの逆。FFTした信号を元に戻すことが出来る。
NTTとは
FFTは実数の計算が生じるため、離散系であるコンピュータ上では誤差が生じる
特に非常に大きな計算をする場合問題になってくる
そこで、整数で全ての計算を行うことで誤差をなくしたものがNTTである
より正確には大きな整数で割ったあまりの上で行うことで逆数やn乗根を定義できるため、大きな整数で割ったあまりで計算を行う
同様にIFFTも整数で行うことができる
DFTを高速化したやつ
DFTを奇数の信号のみ、偶数の信号のみ取り出してDFTした後、それらを合わせると、元の信号をDFTしたものと同じ結果になる
半分にしたものをさらに半分にして同様なことを繰り返すと、結局普通にDFTするより速くなる
何度もサイズを半分にするので、元のデータがちょうどいい数(1024とか256とか)だとやりやすい
IFFTとは
FFTの逆。FFTした信号を元に戻すことが出来る。
NTTとは
FFTは実数の計算が生じるため、離散系であるコンピュータ上では誤差が生じる
特に非常に大きな計算をする場合問題になってくる
そこで、整数で全ての計算を行うことで誤差をなくしたものがNTTである
より正確には大きな整数で割ったあまりの上で行うことで逆数やn乗根を定義できるため、大きな整数で割ったあまりで計算を行う
同様にIFFTも整数で行うことができる
こういち
2021/6/15 13:00
◆.Id/aHiU36hu
FFTは何が嬉しいのか
信号に含まれる周波数成分が分かる
現実で手に入る信号には様々な周波数の成分が含まれている
そのため、そこから必要な信号のみを取り出すといったことが出来る。
あるいは、どのような成分が含まれているかを調べることが出来る
これだけで十分に価値がある
畳み込み演算が高速に行える
畳み込み演算とは何ぞやという疑問は一旦置いておく
この畳み込み演算を使うことでディジタルフィルタを作ることができたり、
変わったところだと大きな桁数の計算が行える。明らかにFFTの使い道を間違えていると思う
信号に含まれる周波数成分が分かる
現実で手に入る信号には様々な周波数の成分が含まれている
そのため、そこから必要な信号のみを取り出すといったことが出来る。
あるいは、どのような成分が含まれているかを調べることが出来る
これだけで十分に価値がある
畳み込み演算が高速に行える
畳み込み演算とは何ぞやという疑問は一旦置いておく
この畳み込み演算を使うことでディジタルフィルタを作ることができたり、
変わったところだと大きな桁数の計算が行える。明らかにFFTの使い道を間違えていると思う
こういち
2021/6/16 12:53
◆.Id/aHiU36hu
実数と虚数の意味(出力側)
簡単のため、周波数が固定で大きさが1の波を考える。
大きさ1の波には、同じ周波数でも1で始まり1で終わるcosと0で始まり0で終わるsinがある。また、これらの中間の中途半端な位置で始まる波もある。
同じ周波数の波が片方の波とどれだけずれているかを位相差と呼ぶ
x軸方向をcos,y軸方向をsinとした平面を考えると、cosとsinの中間の位相差を持った波を矢印で表現できる。これをフェーザという。
また、cos成分を実部、sin成分を虚部とした複素数を考えると、計算がしやすくなる。
つまり、出力の実部と虚部はそれぞれcos成分,sin成分ということになる。
簡単のため、周波数が固定で大きさが1の波を考える。
大きさ1の波には、同じ周波数でも1で始まり1で終わるcosと0で始まり0で終わるsinがある。また、これらの中間の中途半端な位置で始まる波もある。
同じ周波数の波が片方の波とどれだけずれているかを位相差と呼ぶ
x軸方向をcos,y軸方向をsinとした平面を考えると、cosとsinの中間の位相差を持った波を矢印で表現できる。これをフェーザという。
また、cos成分を実部、sin成分を虚部とした複素数を考えると、計算がしやすくなる。
つまり、出力の実部と虚部はそれぞれcos成分,sin成分ということになる。
こういち
2021/6/16 12:53
◆.Id/aHiU36hu
入力の実部と虚部
音声などの信号は実数しかとり得ないが、場面によっては複素数になる場合もある。
例えば、FFTした信号をさらにFFTしたい場合など。
実数しか扱わない場合は虚部は無視してよい。
音声などの信号は実数しかとり得ないが、場面によっては複素数になる場合もある。
例えば、FFTした信号をさらにFFTしたい場合など。
実数しか扱わない場合は虚部は無視してよい。
こういち
2021/6/16 12:56
◆.Id/aHiU36hu
位相とかには興味ないので大きさだけ知りたい
音声とかだと、人間の耳で位相差を感知することは出来ないため、大きさだけ知りたいこともある。
その場合、複素数の絶対値を用いる
複素数の絶対値は、平面上のベクトルの長さなので、三平方の定理で求まる。
sqr(実部*実部+虚部*虚部)
ちなみに、位相差はあーたんを用いると求まる。
ATAN(虚部,実部)
音声とかだと、人間の耳で位相差を感知することは出来ないため、大きさだけ知りたいこともある。
その場合、複素数の絶対値を用いる
複素数の絶対値は、平面上のベクトルの長さなので、三平方の定理で求まる。
sqr(実部*実部+虚部*虚部)
ちなみに、位相差はあーたんを用いると求まる。
ATAN(虚部,実部)
さすらいの名無し
2021/6/16 16:59
◆LWMA5UzCJb3e
高度サウンドユニットなしorMkII以前でもフーリエ変換が使えるってこと?
こういち
2021/6/16 18:07
◆.Id/aHiU36hu
さすらいの名無しさん
FFTも単なる計算なので、自分で実装すれば使えなくはないと思います。
ただ、プチコンはプログラムを書かない方が速い言語なので、高度サウンドユニットほどの速度は出ませんが。
いずれDFT/FFT/NTTの仕組みについても触れていく予定ではあります。
FFTも単なる計算なので、自分で実装すれば使えなくはないと思います。
ただ、プチコンはプログラムを書かない方が速い言語なので、高度サウンドユニットほどの速度は出ませんが。
いずれDFT/FFT/NTTの仕組みについても触れていく予定ではあります。
こういち
2021/6/21 22:17
◆.Id/aHiU36hu
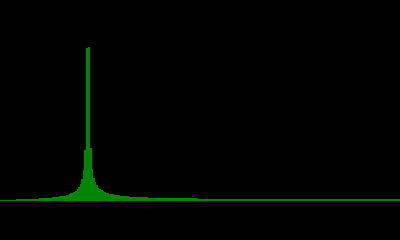
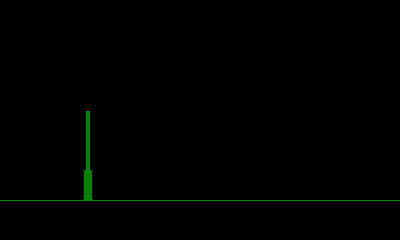
変な信号が出てしまうと困るため、窓関数というものを使います。
窓関数は、端の要素には0に近い値、中央の要素には1に近い値を掛けることで、信号の端と端をなめらかに繋ぐ効果があります。
画像は窓関数のブラックマン窓を使い、111周期分のcos波をFFTしたものです。
もちろん、窓関数を掛けると元の波形とは形が変わってしまいますが、窓関数を使わない場合と比べて余計な信号が出ないため、使わないよりは良い結果になります。
窓関数は、ハニング窓、ハミング窓、ブラックマン窓などが存在し、ハニング窓<ハミング窓<ブラックマン窓の順に余計な信号を軽減する効果が大きくなります。
ただし、余計な信号を軽減する効果が大きい窓は、波形の変形も大きいので注意です。
窓関数は、端の要素には0に近い値、中央の要素には1に近い値を掛けることで、信号の端と端をなめらかに繋ぐ効果があります。
画像は窓関数のブラックマン窓を使い、111周期分のcos波をFFTしたものです。
もちろん、窓関数を掛けると元の波形とは形が変わってしまいますが、窓関数を使わない場合と比べて余計な信号が出ないため、使わないよりは良い結果になります。
窓関数は、ハニング窓、ハミング窓、ブラックマン窓などが存在し、ハニング窓<ハミング窓<ブラックマン窓の順に余計な信号を軽減する効果が大きくなります。
ただし、余計な信号を軽減する効果が大きい窓は、波形の変形も大きいので注意です。
あんちもん
2021/7/19 20:57
◆8qCJSJ1bKTIQ
コメントを書く
- こちらは「プチコン3号」「プチコンBIG」など、プチコンシリーズに関する話題を扱ったコミュニティです
- プチコンシリーズにまったく関係ない書き込みはご遠慮下さい。削除の対象となります
- こちらにはその他のゲームや雑談のコミュニティはなく、作る予定もありません (ひとりで管理できないため)。ごめんなさい
- ユーザー登録なしで書き込みができます
- 秘密の合い言葉は成りすましの防止 (トリップ機能)、書き込みの編集時の本人認証に使用します
- 秘密の合い言葉に他人に推測されやすい言葉、他サービスと同じパスワードは入力しないでください。
- 書き込むと、投稿時に入力したお名前と秘密の暗号が記憶され、ログイン状態になります