Petitverse

有限インパルス応答(FIRフィルタ)について
有限インパルスとか高校数学とか難しそうなことを書きましたが、ディジタルフィルタ自体はシンプルです。

k番目までの入力の列(一般的には音声波形や画素の列(画像)ですが、今回はゲーム等を対象にしているので画素の時間変化やセンサ,ボタン入力等になると思います)X[k+1]があった場合、フィルタ適用後のk番目の出力Y[k]は要素M+1の配列b[M+1]を用いて以下のように計算できます。

Y[k]=0
for i=0 to M
INC Y[k],X[k-i]*b[i]
next i

この配列bの中身を変えることで様々な面白いことが出来ます。

ね、簡単でしょ？

具体的なプログラム例を挙げてみます。

例えば、Aボタンを押している間は画面が白,押していないときは画面が黒になるような、連打したら目に悪そうなプログラムがあったとします。

これにディジタルフィルタを適用すると目に優しく出来そうです。

フィルタはいろいろ考えられますが、とりあえずM=63で全ての値が1/64のシンプルなフィルタを使います。(つまり、過去64入力の平均です)

以下は3号用のプログラムです。4やPi Starterでも少し変えれば動くと思います。

ACLS
XSCREEN 1

VAR M%=63
DIM X#[M%+1],B#[M%+1]
VAR Y#=0
VAR K%=0,J%
VAR W%=400,H%=240 '画面サイズ

FILL B#,1.0/64

WHILE 1
　WAIT 1
'ボタンの入力
　IF 16==(BUTTON() AND 16) THEN
　　X#[K%]=255
　ELSE
　　X#[K%]=0
　ENDIF
　'フィルタの計算
　Y#=0
　FOR J%=0 TO M%
　　Y#=Y#+X#[(K%-J%+M%)MOD M%]*B#[J%]
　NEXT J%
　'描画
　GFILL 0,0,W%,H%,RGB(ROUND(Y#),ROUND(Y#),ROUND(Y#))
　K%=K%+1
　IF K%>M% THEN K%=0
WEND

無限インパルス応答(IIRフィルタ)について

FIRフィルタではk番目までの入力X[k+1]の列と要素M+1の配列b[M+1]からk番目の出力Y[k]を計算しましたが、IIRフィルタではそれに加えてk個の出力Y[k]と要素N+1の配列a[N+1]を使って以下のように計算します。

Y[k]=0
for i=1 to N
INC Y[k],Y[k-i]*a[i]
next i
for i=0 to M
INC Y[k],X[k-i]*b[i]
next i

ここで、a[0]は常に1です。
先のFIRフィルタはIIRフィルタのうちa[1〜N]が0のものと見ることもできます。

例によって具体的なプログラム例を挙げてみます。

FIRフィルタのときのプログラムと同じプログラムをIIRフィルタで実現してみます。

フィルタはM=0,N=1でa[1]=0.9,b[0]=0.1のフィルタを使います。

3号用のプログラムです。4やPi Starterでも少し変えれば動くと思います。

ACLS
XSCREEN 1

VAR X#
VAR A1#=0.9,B0#=0.1
VAR Yk#=0,Yk1#=0 'Y[k],Y[k-1]
VAR W%=400,H%=240 '画面サイズ

WHILE 1
　WAIT 1
'ボタンの入力
　IF 16==(BUTTON() AND 16) THEN
　　X#=255
　ELSE
　　X#=0
　ENDIF
　'フィルタの計算
　Yk#=A1#*Yk1#+B0#*X#
　'描画
　GFILL 0,0,W%,H%,RGB(ROUND(Yk#),ROUND(Yk#),ROUND(Yk#))
　Yk1#=Yk#
WEND

これまで簡単なフィルタについて見てきましたが、次のような疑問を持ったかもしれません。

- 実際に配列の中身はどのような値にすれば良いのか
- どのような場面でどのようなフィルタを使えば良いのか

ようこそ。闇の世界へ

フィルタの種類について

ところで、世の信号には様々な周波数信号が含まれています。
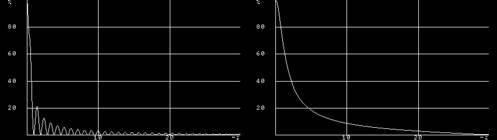
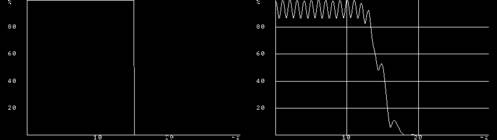
フィルタの役割は特定の周波数の信号を増やしたり減らしたりすることですが、具体的にどの周波数をどの程度減らすのかを表したものを周波数特性と言います。

ここで、先に使用したフィルタの周波数特性を計算すると画像のようになります。

低い周波数はあまり減らず、高い周波数が大きく減っているのが分かると思います。
このように低い周波数(Low)を通す(Pass)フィルタ(Filter)をLPFと言います。
一般的には以下のようなフィルタがよく使われます。

- 低域通過フィルタ(LPF)
- 高域通過フィルタ(HPF)
- 帯域通過フィルタ(BPF)

設計方法にもよりますが、HPFやBPFはLPFを変換して設計するのがセオリーです。
以降、特に断りのない場合はLPFについて解説します。

周波数特性の求め方
http://petitverse.hosiken.jp/community/petitcom/topic/?read=1747&ukey=0

フィルタの性能について

理想的なLPFの周波数特性は左の画像のようになります。
このうち、利得が100%の部分を通過域,0%の部分を阻止域と言います。
また、通過域から阻止域に変わる周波数をカットオフ周波数(遮断周波数)と言います。

理想的なLPFの話をしましたが、完全に理想的なLPFを作るのはまず不可能です。
そのため、実際には右のような特性になります。

一般的に
通過域の特性が平坦であること
阻止域の利得が小さいこと
が望ましい特性とされています。

さて、フィルタでは周波数特性も重要ですが、入力した信号がどれだけ遅れるかも重要になります。
周波数特性と同様にどの周波数がどれだけ遅れるかを表したものを位相特性と言います。

当然ながら、信号は遅れないに越したことはないですが、信号が遅れないLPFを作るのはまず不可能です。

一般的には次のような特性が望まれます。
通過域での位相特性が直線的であること

一般的には他の項目より求められませんが、ゲームでは次の特性も重要になると思います。
位相特性がなるべく小さいこと

有限の計算では全ての特性を追求するのは難しいため、どの特性を重視して設計するかが重要です。
各特性に優れている特性のフィルタは以下の名前が付いています。
通過域の特性が平坦:バターワース特性
阻止域の利得が小さい:チェビシェフ/逆チェビシェフ/連立チェビシェフ特性
位相線形性が大きい:ベッセル特性
位相特性が小さい:最小位相特性

…とまあ色々書きましたが、上に挙げた特性は最小位相特性を除きFIRフィルタではあまり関係ありません。(元々アナログフィルタで使われていた用語で、IIRフィルタの方はアナログフィルタの特性を変換して設計されるのがセオリーなのでよく使う)

Z変換について

FIRフィルタは遅延演算子Z(Dの場合もある)を利用して次のように表記されることもあります。

Y(z)=a(0)+a(1)*z^-1+a(2)*z^-2+…a(n)*z^-n

これはFIRフィルタの式にZ変換という変換を行った形になります。
このような形の式が出て来たらFIRフィルタのことなんだなと思うようにしましょう。

畳み込みのプロ・畳小宮の存在だ。

FIRフィルタはFFTやNTTを使って高速に計算できる場合があります。
具体的には、k番目までの入力X[k+1]の列に要素N+1のFIRフィルタa[N+1]を適用した出力Y[k+N+2]はFFTを使って以下のように表すことが出来ます。
Y=L*IFFT(FFT(X)*FFT(A))
ここでLはYの要素数です。

さあ，FIRフィルタの高速化開始だ！とあなたは意気込んでいるところかもしれないが，ちょっと待ってほしい．二つだけ先に忠告しておくことがある．
一つは要素数を十分に確保しておくことだ。要素数が不足している場合、入力あるいはフィルタが繰り返されているものとして計算される。
もう一つはFFTの式には複数の流派があることだ。プチコンの場合はIFFTのあとに配列の要素Lを掛ける必要があるが、多くの実装ではLを掛けなくて良い流派を採用している場合が多い。いずれにせよ事前に確認しておく必要があるだろう。
http://petitverse.hosiken.jp/community/petitcom/topic/?read=1841&ukey=0

線形位相フィルタと遅延について

フィルタの特性で、通過域での位相特性が直線的であることが望ましいと書きましたが、全ての領域で位相特性が完全に直線である特性を線形位相特性と言い、ある種の理想的な特性と言えます。
要素数NのFIRフィルタa[N]において、以下の条件のいずれかを満たす場合線形位相特性を持ちます。逆に、どちらも満たさない場合、線形位相特性になりません。

a[i]=a[N-i-1]
a[i]=-a[N-i-1]

最初に例として出した過去64要素の平均を取るフィルタは1番目の条件を満たすため、線形位相特性を持ちます。

線形位相特性は理想的な特性ではありますが、必ずN/2の遅延が生じます。

そのため、遅延の少ないフィルタを設計しようとした場合、線形位相特性は諦める必要があります。(近似的に直線的な位相特性を持たせることは可能。難しいけど)

線形位相FIRフィルタの設計について(窓関数法)

線形位相FIRフィルタを設計します。
後述しますが、最小位相フィルタは線形位相フィルタを変換することで作ることが出来ます(主に低次数での設計法)
ともかく線形位相フィルタが必要なため、まずは最も簡単な窓関数法を使うことにします。

まず、理想的なフィルタの係数は次の式で表すことが出来ます。(導出は省略)

b[n]=sin(2*Pi()*n*f)/n/Pi()

ここで、fは正規化されたカットオフ周波数であり、カットオフ周波数をサンプリング周波数で割ることで求めることが出来ます。

この係数は±∞の範囲なため、窓関数を掛けて有限要素で打ち切ってやります。
窓関数は低次数ではハニング窓やハミング窓,高次数ではブラックマン窓が使われます。


負の要素が存在するとプログラムで表しづらい(正確に言うと因果性ってのが成り立たなくなるのがまずい)ため、要素を後ろにずらして0から始まるようにします。

SmileBASICのFFTWFNでは最初から要素を後ろにずらした窓関数が生成されるので、これで良いですが何故かキリの良い要素数しか使えないらしいので自作するのが無難です。
全く関係ないですが、最近二項係数窓という窓関数が気になってます(用途としてはブラックマン窓よりさらに上の、無限として扱えるレベルの要素数で使う。ちなみに、二項係数窓をそのままフィルタの係数として扱ったものが画像処理で使われるガウシアンフィルタ)

零点(根)とベアストウ法

FIRフィルタはz変換を使って
Y(z)=a(0)+a(1)*z^-1+a(2)*z^-2+…a(n)*z^-n
のような表現が出来ると言いましたが、ここで
Y(z)=0の解を零点(数学的には根)と言い、フィルタの性質を知るのに有効だったりします。
どのように有効かはやらない夫のサイトを見るのが早いですが、最小位相フィルタについては「全ての零点の絶対値が1以下」という条件を満たせば最小位相フィルタになることが知られています。
http://www.ic.is.tohoku.ac.jp/~swk/lecture/yaruodsp/dfanalysis.html

そんなわけで、Y(z)=0を求める必要があるわけですが、「5次以上の代数方程式は解の方程式が存在しない」というのを聞いたことがある人も多いと思います。
だからというわけではないですが、実際Y(z)=0を求めるのは難しいです。
ですが安心してください。コンピュータの計算速度を利用すれば反復手法によって次数3桁ぐらいなら近似的な解を求めることが出来ます。

根を求めるアルゴリズムはいくつかありますが、ディジタルフィルタの場合はベアストウ法が便利です。(そして何よりあのフェルミウム湾さんも賞賛してる)
ベアストウ法は係数が全て実数の場合に使用可能なアルゴリズムで、複素数の計算が最小で、複素解の場合、共役な複素数とセットで解が求まるという特徴があります。
http://petitverse.hosiken.jp/community/petitcom/topic/?read=1792&ukey=0

def bairstow(double a[],double ro[],double jo[],int n)
　var cnt%=0,i,j
　var d#
　fill bair1,0:fill bair2,0
　var a0#=a[0]
　aryop 3,a,a,a0%
　while n>3
　　var p#,q#
　　var dp#=1,dq#=1
　　p#=q#=0
　　while abs(dp#)>1e-10||abs(dq#)>1e-10
　　　bair1[0]=a[0]
　　　bair1[1]=a[1]-p#*a[0]
　　　bair2[0]=bair1[0]
　　　bair2[1]=bair1[1]-p#*bair1[0]
　　　for j=2 to n-1
　　　　bair1[j]=a[j]-p#*bair1[j-1]-q#*bair1[j-2]
　　　　bair2[j]=bair1[j]-p#*bair2[j-1]-q#*bair2[j-2]
　　　next j
　　　var r#=bair2[n-3]*bair2[n-3]-(bair2[n-2]-bair1[n-2])*bair2[n-4]
　　　dp#=(bair1[n-2]*bair2[n-3]-bair1[n-1]*bair2[n-4])/r#
　　　dq#=(-bair1[n-2]*(bair2[n-2]-bair1[n-2])+bair1[n-1]*bair2[n-3])/r#
　　　p#+=dp#
　　　q#+=dq#
　　wend
　　d#=p#*p#-4*q#
　　if d#>0 then
　　　ro[cnt%]=(-p#+sqr(d#))/2
　　　ro[cnt%+1]=(-p#-sqr(d#))/2
　　　jo[cnt%]=jo[cnt%+1]=0
　　　cnt%=cnt%+2
　　else
　　　ro[cnt%]=-p#/2
　　　jo[cnt%]=sqr(-d#)/2
　　　cnt%=cnt%+1
　　endif
　　for i=0 to n-1
　　　a[i]=b[i]
　　next i
　　n=n-2
　wend
　if 3==n then
　　d#=a[1]*a[1]-4*a[2]
　　if d>0 then
　　　ro[cnt%]=(-a[1]+sqr(d#))/2
　　　ro[cnt%+1]=(-a[1]-sqr(d#))/2
　　　jo[cnt%]=jo[cnt%+1]=0
　　　cnt%=cnt%+2
　　else
　　　ro[cnt%]=-a[1]/2
　　　jo[cnt%]=sqr(-d#)/2
　　　cnt%=cnt%+1
　　endif
　else
　　ro[cnt%]=-a[1]
　　jo[cnt%]=0
　　cnt%=cnt%+1
　endif
　return cnt%
end

最小位相フィルタについて

以下の3つの性質が成り立つとします。

1.ある複素数c=a+jbにおいて、cと1/cの少なくともどちらかは絶対値が1以下になる
2.線形位相フィルタにおいて、ある根をrとしたとき、1/rも根となる
3.ある実係数FIRフィルタFにおいて、根が全てRの根の逆数であるようなフィルタIは定数倍を除いてRと同じ周波数特性を持つ

1は簡単に証明できます。
線形位相フィルタのz変換形は相反多項式と呼ぶらしく(フェルミウム湾さん情報)、2の性質も成り立つそうです。
https://ja.wikipedia.org/wiki/%E7%9B%B8%E5%8F%8D%E5%A4%9A%E9%A0%85%E5%BC%8F#%E6%80%A7%E8%B3%AA_2
3は成り立ってくれると嬉しい。


性質1,2より、線形位相フィルタは根の絶対値が1以下であるフィルタFと根の絶対値が1以上であるフィルタG,根が1であるフィルタnを用いて
nFG
と表すことが出来る。
性質3が成り立つと仮定すると、GとFは定数倍を除いて同じ周波数特性を持つため、
nF^2
は定数倍を除いて元の線形位相フィルタと同じ周波数特性を持つ。
nF^2
は全ての根の絶対値が1以下であるため、最小位相フィルタとなる。