プチコン 非公式コミュニティ
トピック
プチコン 非公式コミュニティ
トピック
ホラムーン
◆uyXAks2Ee1EU
2018/9/15 8:47
2018/9/15 8:47
協力
プログラミングの問題をください
上達するには実践が何よりの近道ですが、プログラミングをしようとしても「何の命令を使えばいいんだ!」となります。
おそらくこれは単純に経験不足&知識不足だと思います。なので必要な命令と条件を書いた問題を提供してほしいです。
例 PRINT命令を使って10+10をさせなさい。ただし、計算式も表示させることとする。(必要な命令・PRINT)
おそらくこれは単純に経験不足&知識不足だと思います。なので必要な命令と条件を書いた問題を提供してほしいです。
例 PRINT命令を使って10+10をさせなさい。ただし、計算式も表示させることとする。(必要な命令・PRINT)
コメント
ツララ
2018/9/15 18:03
◆ArUdBYOYME1V
[問題]
PRINT命令を「使わない」で
ACLS
PIRNT "HELLO WORLD!"
を実行した時と「同じ見た目の画面」になるプログラムを書きなさい。
必要な命令:G系のグラフィック関連の命令全般
条件:特に無し
なお、プログラム終了時のフォルダ名とカーソル点滅の表示は無視して構わない。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
同じ出力を別の色んな方法で試してみるのって基本中の基本ですし
「〇〇だから出来ない」なんて言い訳が慣れた人の目にはどう映ってるのか
実感出来ると思いますよん。
PRINT命令がコンソール画面で、他の画面で言う何命令に相当する働きをしているのかを理解していれば
後はリソースをどこから持って来るのか、それとも自前で用意するのか
ご自由にって感じですかね。
PRINT命令を「使わない」で
ACLS
PIRNT "HELLO WORLD!"
を実行した時と「同じ見た目の画面」になるプログラムを書きなさい。
必要な命令:G系のグラフィック関連の命令全般
条件:特に無し
なお、プログラム終了時のフォルダ名とカーソル点滅の表示は無視して構わない。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
同じ出力を別の色んな方法で試してみるのって基本中の基本ですし
「〇〇だから出来ない」なんて言い訳が慣れた人の目にはどう映ってるのか
実感出来ると思いますよん。
PRINT命令がコンソール画面で、他の画面で言う何命令に相当する働きをしているのかを理解していれば
後はリソースをどこから持って来るのか、それとも自前で用意するのか
ご自由にって感じですかね。
ホラムーン
2018/9/15 22:37
◆uyXAks2Ee1EU
皆さんありがとうございます。
今日はプチコンはもう触れないのでまた後日に解答しますね。
個人的にはツララさんが珍しく素直でまともな事を言っててビックリなのですが、それだけ真面目に答えてくださってるのかな?とか思うと勝手に嬉しくなってきます。
という訳でもう寝ます!ありがとうございます!
今日はプチコンはもう触れないのでまた後日に解答しますね。
個人的にはツララさんが珍しく素直でまともな事を言っててビックリなのですが、それだけ真面目に答えてくださってるのかな?とか思うと勝手に嬉しくなってきます。
という訳でもう寝ます!ありがとうございます!
クロマリオ
2018/9/16 13:46
◆jST6XW8BxBax
プログラム内でGRPとDATの見分け方存在しない問題
ろどに
2018/9/16 15:07
◆vU1zN5Kpe4Y3
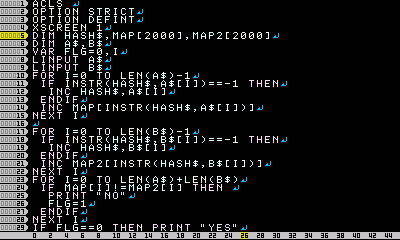
2つの文字列A$,B$について、
A$を並び替えるとB$と一致するかどうか判定し
一致する場合は「YES」を
どう並び替えても一致しない場合は「NO」を
出力するプログラムを作成してください。
A$,B$はそれぞれLINPUTで与えるものとします。
また、文字列の長さは最大で1000文字程度です。
[入力例1]
ABCDEF
FEDCBA
[出力例1]
YES
[入力例2]
-12334
33-4
[出力例2]
NO
[必要な命令]
LINPUT(INPUTではないことに留意)
PRINT(あるいは「?」)
IF,FORなど制御命令
LEN,ASCなど適当な文字列操作
適当な配列操作
CLS等画面消去は必要ありません。
A$を並び替えるとB$と一致するかどうか判定し
一致する場合は「YES」を
どう並び替えても一致しない場合は「NO」を
出力するプログラムを作成してください。
A$,B$はそれぞれLINPUTで与えるものとします。
また、文字列の長さは最大で1000文字程度です。
[入力例1]
ABCDEF
FEDCBA
[出力例1]
YES
[入力例2]
-12334
33-4
[出力例2]
NO
[必要な命令]
LINPUT(INPUTではないことに留意)
PRINT(あるいは「?」)
IF,FORなど制御命令
LEN,ASCなど適当な文字列操作
適当な配列操作
CLS等画面消去は必要ありません。
こういち
2018/9/16 19:37
◆ou0jbJnEJ0Kb
時間制限ないとは言えろどにさんのやつがわりとガチ勢な件。
ちょっと考えてきます。
ちょっと考えてきます。
キルル2
2018/9/16 22:00
◆rGE712Ruejv7
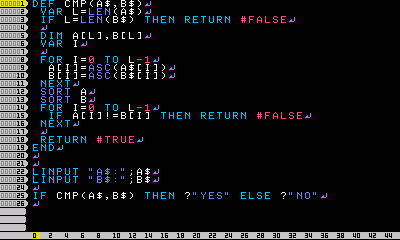
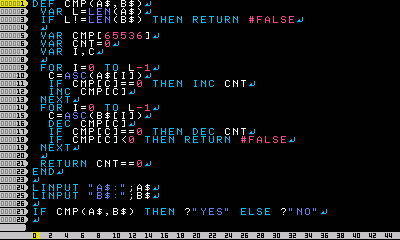
ろどにさんの問題はそこまで難しくないと思います
次の投稿でO(n)の答えを示します
次の投稿でO(n)の答えを示します
test
2018/9/17 12:25
◆oJ2RFHFIpVGF
ちょっとだけ難しい問題を。
問題:
INPUTで入力した数値を素因数分解して以下の例のように表示するプログラムを作成しなさい。
例:
60=2×2×3×5
15=3×5
必要な命令:
input print while if break
問題:
INPUTで入力した数値を素因数分解して以下の例のように表示するプログラムを作成しなさい。
例:
60=2×2×3×5
15=3×5
必要な命令:
input print while if break
ホラムーン
2018/9/17 14:49
◆uyXAks2Ee1EU
>>testさん
中一の僕には素因数分解なんて分からないや(´・ω・`)
中一の僕には素因数分解なんて分からないや(´・ω・`)
オワたず
2018/9/17 16:16
◆w7BXxYlkW2NJ
ホラムーンさん>>まず素数はわかりますかね?
ホラムーン
2018/9/17 17:41
◆uyXAks2Ee1EU
>>オワたず
分かりますよ、1とその数以外で割れない数ですよね。
一応成績はオール五なので習ってる内容なら数学に限らず理解してます。
分かりますよ、1とその数以外で割れない数ですよね。
一応成績はオール五なので習ってる内容なら数学に限らず理解してます。
- 1
- 2
コメントを書く
- こちらは「プチコン3号」「プチコンBIG」など、プチコンシリーズに関する話題を扱ったコミュニティです
- プチコンシリーズにまったく関係ない書き込みはご遠慮下さい。削除の対象となります
- こちらにはその他のゲームや雑談のコミュニティはなく、作る予定もありません (ひとりで管理できないため)。ごめんなさい
- ユーザー登録なしで書き込みができます
- 秘密の合い言葉は成りすましの防止 (トリップ機能)、書き込みの編集時の本人認証に使用します
- 秘密の合い言葉に他人に推測されやすい言葉、他サービスと同じパスワードは入力しないでください。
- 書き込むと、投稿時に入力したお名前と秘密の暗号が記憶され、ログイン状態になります