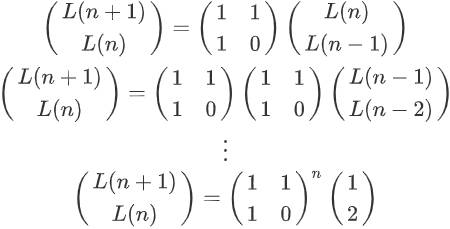�v�`�R�� ������R�~���j�e�B
�g�s�b�N
�v�`�R�� ������R�~���j�e�B
�g�s�b�N
��������
��.Id/aHiU36hu
2020/9/16 7:42
2020/9/16 7:42
�R���e�X�g
���(Lucas Number)
����N���^������̂ŁAN�Ԗڂ̃����J����20123�Ŋ��������܂�����߂Ȃ����B
�������A�����J���Ƃ͈ȉ��̎��ŕ\����鐔�ł��B
L(N+1)=L(N)+L(N-1)
L(N)=L(N)
L(0)=2
L(1)=1
�������A�����J���Ƃ͈ȉ��̎��ŕ\����鐔�ł��B
L(N+1)=L(N)+L(N-1)
L(N)=L(N)
L(0)=2
L(1)=1
�R�����g
��������
2020/9/16 7:43
��.Id/aHiU36hu
���͈͂ȉ��̂悤�ɗ^�����܂��B
N
����
0<=N<=2147483647
�Ȃ��A���O�m���������Ɠ���Ǝv����̂ŁA����̓q���g���^�����܂��B
N
����
0<=N<=2147483647
�Ȃ��A���O�m���������Ɠ���Ǝv����̂ŁA����̓q���g���^�����܂��B
SatoshiMcCloud
2020/9/16 18:44
��Z1qfV11i63Jr
L(N)=L(N)
���͂ǂ������Ӑ}�c�H
���͂ǂ������Ӑ}�c�H
SatoshiMcCloud
2020/9/17 12:19
��Z1qfV11i63Jr
<�ؖ�>
���鐔20123��M�ƒu�������A
F(N)=L(N) mod M
�Ƃ���B
(i)�萔T�ɑ��A
F(N)=F(N+T)
F(N-1)=F(N-1+T)
�����藧�ꍇ�A
(A op B) mod C=((A mod C)op B)mod C
�̐�������A
F(N+1)=L(N+1) mod M
=(L(N)+L(N-1)) mod M
=((L(N) mod M)+L(N-1))mod M
=(F(N)+L(N-1))mod M
=(F(N)+(L(N-1) mod M)) mod M
=(F(N)+F(N-1))mod M
=(F(N+T)+F(N-1+T)) mod M
=F(N+1+T)
(ii) F(N)=L(N) mod M
����AF(N)�̒l��M�p�^�[�������Ȃ��B
F(N)��F(N-1)�̒l����肤��l�̑g�ݍ��킹�͍ő�M^2�ł��邱�Ƃ���A0<=N<=M^2�͈̔͂ŕK��1��ȏ�� F(N)=F(N+T) ���� F(N-1)=F(N-1+T) �̑g�ݍ��킹���o�����邱�ƂɂȂ�B
(iii)�ȏ�ɂ��AL(N)��M�̗]��͕K�������������B����T��T<=M^2�ł���B
���鐔20123��M�ƒu�������A
F(N)=L(N) mod M
�Ƃ���B
(i)�萔T�ɑ��A
F(N)=F(N+T)
F(N-1)=F(N-1+T)
�����藧�ꍇ�A
(A op B) mod C=((A mod C)op B)mod C
�̐�������A
F(N+1)=L(N+1) mod M
=(L(N)+L(N-1)) mod M
=((L(N) mod M)+L(N-1))mod M
=(F(N)+L(N-1))mod M
=(F(N)+(L(N-1) mod M)) mod M
=(F(N)+F(N-1))mod M
=(F(N+T)+F(N-1+T)) mod M
=F(N+1+T)
(ii) F(N)=L(N) mod M
����AF(N)�̒l��M�p�^�[�������Ȃ��B
F(N)��F(N-1)�̒l����肤��l�̑g�ݍ��킹�͍ő�M^2�ł��邱�Ƃ���A0<=N<=M^2�͈̔͂ŕK��1��ȏ�� F(N)=F(N+T) ���� F(N-1)=F(N-1+T) �̑g�ݍ��킹���o�����邱�ƂɂȂ�B
(iii)�ȏ�ɂ��AL(N)��M�̗]��͕K�������������B����T��T<=M^2�ł���B
SatoshiMcCloud
2020/9/17 23:22
��Z1qfV11i63Jr
�ł������Ă݂�ƁAM^2�ɑ��Ď���T�����Ȃ菬�������l�ł��邱�Ƃ������̂́A�����ɉ𖾂ł����c�B
�i���ɏo�Ă����ł��AM=20123�ɑ���T=40248�����j
�i���ɏo�Ă����ł��AM=20123�ɑ���T=40248�����j
SatoshiMcCloud
2020/9/18 18:08
��Z1qfV11i63Jr
����ɐF�X���ׂĂ݂܂����B
(i)�t�B�{�i�b�`����F(n)�Ƃ���Ɓi��̏ؖ���F�Ƃ͖��W�ł��j�A�t�B�{�i�b�`���ƃ����J���̊Ԃɂ�
L(n)=F(n-1)+F(n+1)
�Ƃ����W�����藧�����ł��B
(ii)�t�B�{�i�b�`����p�Ŋ������]��́Ap��f������5�ł�2�ł��Ȃ��Ƃ��āA
�Ep��5�Ŋ������]�肪1�܂���4�Ȃ�A������p-1�̖�
�Ep��5�Ŋ������]�肪2�܂���3�Ȃ�A������2(p+1)�̖�
�Ƃ�������������悤�ł��B
(iii)��������A�����J����p�Ŋ��������̓t�B�{�i�b�`����p�Ŋ��������̎����ƈ�v���邩���A�Ƃ����\�z�����Ă��܂��B
����̃P�[�X��p=20123�ŁAp��5�Ŋ������]���3�B������2(20123+1)=40248�̖Ɠ����܂��B
�����A�������A�ɂ����������ƃs�^����v�����I�I�I
(i)�t�B�{�i�b�`����F(n)�Ƃ���Ɓi��̏ؖ���F�Ƃ͖��W�ł��j�A�t�B�{�i�b�`���ƃ����J���̊Ԃɂ�
L(n)=F(n-1)+F(n+1)
�Ƃ����W�����藧�����ł��B
(ii)�t�B�{�i�b�`����p�Ŋ������]��́Ap��f������5�ł�2�ł��Ȃ��Ƃ��āA
�Ep��5�Ŋ������]�肪1�܂���4�Ȃ�A������p-1�̖�
�Ep��5�Ŋ������]�肪2�܂���3�Ȃ�A������2(p+1)�̖�
�Ƃ�������������悤�ł��B
(iii)��������A�����J����p�Ŋ��������̓t�B�{�i�b�`����p�Ŋ��������̎����ƈ�v���邩���A�Ƃ����\�z�����Ă��܂��B
����̃P�[�X��p=20123�ŁAp��5�Ŋ������]���3�B������2(20123+1)=40248�̖Ɠ����܂��B
�����A�������A�ɂ����������ƃs�^����v�����I�I�I
��������
2020/9/18 20:22
��.Id/aHiU36hu
SatoshiMcCloud����
�������͋M�������c�܂��܂��m��Ȃ����Ƃ����肻�����c
���Ȃ݂ɁA�t�B�{�i�b�`�f���������ɑ��݂��邩�ǂ����͖�������肾�����ł��B
�������͋M�������c�܂��܂��m��Ȃ����Ƃ����肻�����c
���Ȃ݂ɁA�t�B�{�i�b�`�f���������ɑ��݂��邩�ǂ����͖�������肾�����ł��B
��������
2020/9/25 6:07
��.Id/aHiU36hu
�V���Ȗ��𓊍e���܂����B
��������܂��B
http://petitverse.hosiken.jp:80/community/petitcom/topic/?read=1580&ukey=0
��������܂��B
http://petitverse.hosiken.jp:80/community/petitcom/topic/?read=1580&ukey=0
��������
2020/9/25 20:33
��.Id/aHiU36hu
�ꉞ�A�����I�łȂ���@��������Ă����B
�����I�łȂ���@1 �������ċA
��`�ʂ�ɍċA��g�ނ��Ƃŋ��߂邱�Ƃ��o���܂��B
DEF L(N)
�@IF N==0 THEN RETURN 2
�@IF N==1 THEN RETURN 1
�@RETURN (L(N-1)+L(N-2)) MOD 20123
END
�������A�����ɑ傫�����߁A���̕��@���ƌv�Z���I��鍠�ɂ͒n�����ŖS���ĂĂ����������Ȃ��ł��B(���炭���̑O��Stack overflow���o�܂���)
���̂��߁A��x�v�Z�����l��z��ɓ���Ă������ƂŁA�����v�Z�������ɍς݈ꎞ�Ԃ����炸�Ɍv�Z���邱�Ƃ��o���܂��B
���̂悤�ɁA��x�v�Z�����l���L�^���čċA���e�N�j�b�N���������ċA�ƌĂт܂��B
�v�Z�ʂ�O(N)�ł��B
�R��@2
�Ƃ�DP
FOR��2�Ԗڂ̃����J�����珇�Ɍv�Z���邱�ƂŁAO(N)�Ōv�Z�ł��܂��B���̂Ƃ��A�v�Z�Ɏg���̂�2�O�܂ł̒l�����Ȃ̂ŁA�ϐ���2�ƈꎞ�ϐ�������Ώ\���ł��B
A=2,B=1,TMP
FOR I=0 TO N
�@TMP=B
�@B=(A+B) MOD 20123
�@A=TMP
NEXT I
PRINT A
�R��@3 �����ċA
�ċA�̎d�����H�v���邱�ƂŁA���������g�킸��DP�Ɠ����v�Z�ʂ������ł��܂��B(���ς�炸Stack Overflow�͂���)
�����I�łȂ���@1 �������ċA
��`�ʂ�ɍċA��g�ނ��Ƃŋ��߂邱�Ƃ��o���܂��B
DEF L(N)
�@IF N==0 THEN RETURN 2
�@IF N==1 THEN RETURN 1
�@RETURN (L(N-1)+L(N-2)) MOD 20123
END
�������A�����ɑ傫�����߁A���̕��@���ƌv�Z���I��鍠�ɂ͒n�����ŖS���ĂĂ����������Ȃ��ł��B(���炭���̑O��Stack overflow���o�܂���)
���̂��߁A��x�v�Z�����l��z��ɓ���Ă������ƂŁA�����v�Z�������ɍς݈ꎞ�Ԃ����炸�Ɍv�Z���邱�Ƃ��o���܂��B
���̂悤�ɁA��x�v�Z�����l���L�^���čċA���e�N�j�b�N���������ċA�ƌĂт܂��B
�v�Z�ʂ�O(N)�ł��B
�R��@2
�Ƃ�DP
FOR��2�Ԗڂ̃����J�����珇�Ɍv�Z���邱�ƂŁAO(N)�Ōv�Z�ł��܂��B���̂Ƃ��A�v�Z�Ɏg���̂�2�O�܂ł̒l�����Ȃ̂ŁA�ϐ���2�ƈꎞ�ϐ�������Ώ\���ł��B
A=2,B=1,TMP
FOR I=0 TO N
�@TMP=B
�@B=(A+B) MOD 20123
�@A=TMP
NEXT I
PRINT A
�R��@3 �����ċA
�ċA�̎d�����H�v���邱�ƂŁA���������g�킸��DP�Ɠ����v�Z�ʂ������ł��܂��B(���ς�炸Stack Overflow�͂���)
�R�����g������
- ������́u�v�`�R��3���v�u�v�`�R��BIG�v�ȂǁA�v�`�R���V���[�Y�Ɋւ���b����������R�~���j�e�B�ł�
- �v�`�R���V���[�Y�ɂ܂������W�Ȃ��������݂͂������������B�폜�̑ΏۂƂȂ�܂�
- ������ɂ͂��̑��̃Q�[����G�k�̃R�~���j�e�B�͂Ȃ��A���\�������܂��� (�ЂƂ�ŊǗ��ł��Ȃ�����)�B���߂�Ȃ���
- ���[�U�[�o�^�Ȃ��ŏ������݂��ł��܂�
- �閧�̍������t�͐��肷�܂��̖h�~ (�g���b�v�@�\)�A�������݂̕ҏW���̖{�l�F�Ɏg�p���܂�
- �閧�̍������t�ɑ��l�ɐ�������₷�����t�A���T�[�r�X�Ɠ����p�X���[�h�͓��͂��Ȃ��ł��������B
- �������ނƁA���e���ɓ��͂��������O�Ɣ閧�̈Í����L������A���O�C����ԂɂȂ�܂�