Petitverse

『2-情体配列』
見てくれてる人が多くなくともいるという事なので続き書きます。
いよいよここから本格的な内容に入ります。創作活動への具体的な応用方法などもお伝えするのでぜひ見てくれると嬉しいですね…。

[情体配列の定義]
事象を配列形式で表記したものを事象配列と言います。
事象配列に情体を掛け合わせたものを情体配列と呼びます。
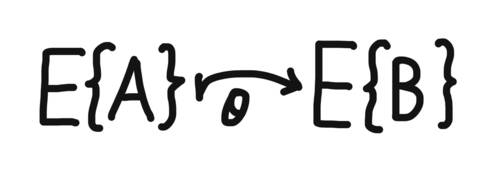
情体配列は以下のように表されます。
[(n-m)φ・ρ^m(x)=(n-m)φ・E^m{A}{B}{C})]
事象配列は一つの事象とカウントするので情体配列も情体とみなします。
また、解釈次元数nの情体配列に含まれる事象配列がm個ある場合、φの解釈次元数はn-mとなります。
例えば、情体配列[φE{A}{B}{C}E{D}{E}{F}]は世界観を表します。
{A}には事象を表す漢字の項が入ります。
なお、印象解析法における解釈する順番(掛ける順番)は、左→右ですが、情体配列の時は事象配列を左→右に解釈してからφの中身を解釈するという特殊な順番になります。
{B}には相対強度比率が入ります。情体全体を見た時、どの事象がどういう比率で目立つのか、を表します。
{C}には漢字項それぞれの素印象を度数法で書き並べます。
情体配列における注意点として、φにはarea関数の情報が入っていますがこのarea関数には漢字項全ての素印象の和が入ります。情体配列のφの中身のarea関数がarea(x,y)だったとしても情体配列を構成する事象配列の項の素印象が全てarea(x,y)とは限りません。
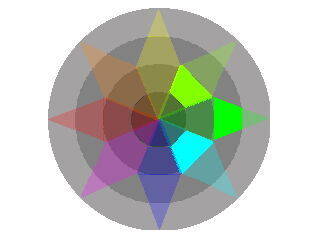
漢字項の素印象の和が存在可能領域からはみ出し、対消滅することがありますが、その場合情体配列自体が存在しないとみなします。

画像は最近計算したやつから抜き出してきたやつです。

[情体配列の加算-基礎]
情体配列同士を加算する時はお互いの項を全て書き並べます。
集合のA∪Bみたいな感じです。
また、共通項が存在するときは互いの強度を足し合わせます。
加算した際に出来上がった情体配列が存在可能領域に収まっているかどうかにも注意。収まっていなかった場合は加算できない情体であるとみなして加算を諦めるか、特殊な操作を用いて加算できるようにすることが必要となります。

[素印象を求める]
対象の情体配列の解釈次元数を指数に持つρで情体配列を割ると素印象になります。

ここら辺の知識は日常生活で簡単なデザインをしたり、計画したことがムードに合っているかどうか(合っていないと素印象が対消滅する)などを調べたりするときなどに使えます。

↑G系命令かな？よく描きましたね…
とりあえず早く情体配列と事象ベクトルの解説を終わらせて作曲で使える段階までいかないとこのトピック立てた意味ないですね。頑張ります。